Ультра-сглаживатель (UltimateSmoother)

Приблизительное время чтения: 11 минут

Сначала мы познакомили вас с суперсглаживателем (SuperSmoother). Потом мы представим вам ультрасглаживатель (UltimateSmoother). Это прорыв, который вы не захотите пропустить!

Сглаживатель — это фильтр низких частот, который пропускает низкочастотные компоненты спектра входных данных практически без изменений и отклоняет или ослабляет высокочастотные компоненты в данных. Отклонение высокочастотных компонентов приводит к получению выходной волны, которая более гладкая, чем входная. В начале своей инженерной карьеры я проектировал фильтры с использованием реальных индукторов и конденсаторов. Этот опыт позволил мне изобрести SuperSmoother, а также UltimateSmoother, о котором я расскажу позже в этой статье.

SuperSmoother (Супер-Сглаживатель)

Цифровой фильтр SuperSmoother был преобразован из аналогового фильтра, имеющего максимально плоскую характеристику низкочастотного фильтра Баттерворта с уменьшенной задержкой. Код EasyLanguage для SuperSmoother показан на вкладке «Функция SuperSmoother в EasyLanguage». Здесь он написан в виде функции, чтобы его можно было использовать в индикаторах и стратегиях так же легко, как скользящее среднее.

SuperSmoother — это фильтр второго порядка с бесконечной импульсной характеристикой (IIR), что означает, что он использует два предыдущих вычисления выходного сигнала фильтра в текущем вычислении отклика фильтра. Определяющим параметром SuperSmoother является критический период. Критический период — это длина волны, которая разделяет полосу пропускания и полосу подавления. Концептуально можно представить его как длину волны, при которой все более длинные волны проходят без изменений к выходу, а все более короткие волны полностью отклоняются на выходе. На самом деле переход от полосы пропускания к полосе задерживания происходит более плавно. Резкость этого перехода в большей степени зависит от порядка фильтра IIR. Для краткости критический период — это входной «период» в коде, приведенном на вкладке «Функция SuperSmoother».

Экспоненциальное скользящее среднее (EMA) — это фильтр IIR первого порядка, использующий только одно предыдущее вычисление. Это сглаживатель, описываемый уравнением:

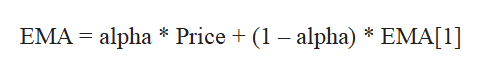
Производительность EMA можно сравнить с производительностью SuperSmoother, если альфа равна 3, деленному на период. Код для построения графика сравнения этих двух сглаживающих функций приведен на вкладке «Отрисовка графика SuperSmoother и EMA». График сравнения показан на рисунке 1.

Очевидно, что SuperSmoother второго порядка (красный цвет) имеет более высокую степень сглаживания, чем EMA первого порядка с эквивалентным критическим периодом (синий цвет). Также очевидно, что оба фильтра имеют задержку по сравнению с входными ценовыми данными. Задержка сглаживающих фильтров является серьезной проблемой для технических трейдеров. Получить правильный ответ не имеет смысла, если он приходит слишком поздно.

Можно разработать сглаживающие фильтры более высокого порядка. Фильтры более высокого порядка усиливают переход от полосы пропускания к полосе задерживания. Однако минус таких фильтров заключается в том, что они вызывают еще большее запаздывание. Поэтому фильтры более высокого порядка редко используются в торговле. Кроме того, расчет фильтров более высокого порядка вызывает ошибки с плавающей запятой на многих торговых платформах. Разумным приближением к отклику фильтра четвертого порядка без получения ошибки с плавающей запятой является сначала отфильтровать данные с помощью SuperSmoother, а затем снова отфильтровать этот результат с помощью SuperSmoother.

Высокочастотный фильтр

Низкочастотные фильтры — не единственный тип фильтров, которые можно использовать. Высокочастотный фильтр второго порядка можно создать, заменив нули в передаточной характеристике фильтра в точке Найквиста (двойной период дискретизации) нулями при нулевой частоте. То есть низкочастотные компоненты входных данных отбрасываются на выходе фильтра, а высокочастотные компоненты проходят на выход без ослабления. Код EasyLaguage для функции фильтра высоких частот приведен на вкладке «Функция фильтра высоких частот в EasyLanguage».

Полосовой фильтр

Другим типом фильтра, который можно разработать, является полосовой фильтр. В фильтре этого типа есть полоса периодов, которые пропускаются на выход практически без ослабления, периоды, длина которых превышает нижний критический период, отбрасываются, а периоды, длина которых превышает верхний критический период, также отбрасываются. Я разработал несколько полосовых фильтров второго порядка, но не рекомендую их использовать, поскольку при использовании таких фильтров возникает соблазн использовать относительно узкую полосу пропускания, чтобы получить выходной сигнал, похожий на синусоиду. Синусоидальный вид получается в результате того, что фильтр пропускает на выход только узкую часть спектра данных. Когда полоса пропускания составляет порядка 25% от центрального периода или менее, сдвиг фазы в полосе пропускания является почти непрерывным. Фазовая характеристика, включая переходные полосы, приближается к 180 градусам. Итак, использование такого фильтра может дать фантастическую синфазную характеристику на некоторое время. Но если характер данных изменится хотя бы немного, выходная волна может дать совершенно неверный торговый сигнал из-за сдвига фазы на 180 градусов. Распознать сдвиг входных данных в режиме реального времени практически невозможно.

Лучший способ создать частотно-полосный фильтр — использовать SuperSmoother с периодом, установленным на верхний критический период полосы пропускания, и высокочастотный фильтр с периодом, установленным на нижний критический период полосы пропускания. Разница между нижним критическим периодом и верхним критическим периодом должна составлять не менее одной октавы. Таким образом, относительное фазовое смещение в полосе пропускания будет практически постоянным. На вкладке «Полосовой фильтр, в EasyLanguage» приведен пример такого полосового фильтра. Полоса пропускания установлена на октаву между периодом цикла 15 тактов и периодом цикла 30 тактов. Эти входные данные можно настроить для получения наилучших результатов для данного набора данных. Выход полосового фильтра представляет собой индикатор типа осциллятора и может использоваться непосредственно в качестве индикатора. Пример отклика фильтра показан на рисунке 2.

Этот полосовой фильтр превосходит полосовой фильтр второго порядка, поскольку обеспечивает более четкие переходы между полосой пропускания и полосами задерживания. Можно представить это так: полосовой фильтр второго порядка применяет один порядок к верхнему краю фильтра и один порядок к нижнему краю фильтра, тогда как этот полосовой фильтр применяет два порядка как к верхнему, так и к нижнему краю полосы.

UltimateSmoother

Как и полосовой фильтр, UltimateSmoother состоит из двух компонентных фильтров. Сглаживающие фильтры всегда имеют задержку в выходе, а задержку следует по возможности избегать. Из своего опыта проектирования аналоговых фильтров я знаю, что фильтры низких частот требуют более крупных индукторов и конденсаторов, а задержка возникает из-за увеличения энергии, необходимой для создания электрического и магнитного полей в этих компонентах. Представьте себе большие низкочастотные динамики для низких частот и крошечные высокочастотные динамики для высоких частот. Эта концепция теряется в цифровых фильтрах, где фильтры представляют собой просто код. Но принцип остается тем же. Вы знаете, что скользящее среднее становится более гладким, чем дольше вы делаете среднее. Это то же самое, что вкладывать больше энергии в фильтр. Вы также знаете, что более длинные скользящие средние имеют большее запаздывание.

UltimateSmoother концептуально имеет нулевую задержку в полосе пропускания и минимальную задержку в полосе перехода, поскольку используется только высокочастотный фильтр. Идея UltimateSmoother описана со ссылкой на схему на рисунке 3. Входные данные математически описываются как всепропускающий фильтр, показанный черным цветом. Отклик высокочастотного фильтра показан синим цветом. Отклик UltimateSmoother является результатом вычитания отклика высокочастотного фильтра из отклика всепропускающего фильтра и показан красным цветом. На очень низких частотах высокочастотный фильтр практически не имеет амплитуды, поэтому в результате вычитания выходной сигнал UltimateSmoother совпадает с входными данными как по амплитуде, так и по задержке. С другой стороны, характеристика фильтра высоких частот практически такая же, как входные данные, и поэтому фильтрация осуществляется путем аннулирования.

Для тех, кто склонен к математике, вычитание фильтра высоких частот из передаточной функции фильтра всепропускающего типа описывается с помощью z-преобразований следующим образом:

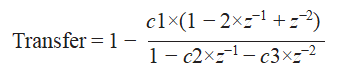
Приведя к общему знаменателю, передаточная функция в замкнутой форме имеет вид:

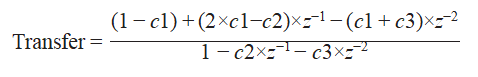
Эта передаточная функция переводится в код EasyLanguage на вкладке «Функция UltimateSmoother в EasyLanguage», которая показывает UltimateSmoother, написанный как функция.

Код EasyLanguage для фильтра UltimateSmoother очень простой, и показан на вкладке «Пример фильтра UltimateSmoother».

Пример UltimateSmoother показан на рисунке 4. Удивительной особенностью UltimateSmoother является отсутствие задержки в полосе пропускания. Отсутствие задержки на рисунке 4 можно сравнить с задержкой SuperSmoother и EMA на рисунке 1. Во всех случаях критический период был установлен на 20 баров. UltimateSmoother может быть применен к любым входным данным, включая другие индикаторы.

Выводы:

1. UltimateSmoother имеет нулевую задержку в полосе пропускания.

2. UtimateSmoother создается путем вычитания отклика высокочастотного фильтра из входных данных.

3. Выходные данные UltimateSmoother не так гладки, как у SuperSmoother, потому что фильтрация осуществляется путем гашения. Амплитудная и фазовая характеристики высокочастотного фильтра в его полосе пропускания не совсем совпадают с характеристиками входных данных.

4. SuperSmoother рекомендуется использовать вместо EMA. В большинстве случаев его также можно использовать вместо простого скользящего среднего.

5. Лучший полосовой фильтр создается путем последовательной фильтрации высокочастотного фильтра и SuperSmoother.

6. Полосовые фильтры должны иметь полосу пропускания, превышающую октаву.

7. Код для UltimateSmoother, SuperSmoother и высокочастотного фильтра предоставляется в виде функций, поэтому их можно вызывать так же легко, как скользящее среднее.

8. Критический период является определяющим параметром для фильтров. Критический период описывает период, который отделяет полосу пропускания от полосы задерживания.

Об Авторе:

Джон Эйлерс — инженер-электрик и технический аналитик, специализирующийся на применении DSP (цифровой обработки сигналов) в торговле. Для получения дополнительной информации см. www.mesasoftware.com.

Дополнительная литература:

1. Элерс, Джон [2014]. «Прогнозирующие и успешные индикаторы», Технический анализ акций и товаров, том 32, январь.
2. [2004]. Кибернетический анализ акций и фьючерсов, John Wiley & Sons.

———————————————
Переведено специально для сайта Finware Technologies, www.finware.ru
Вы можете свободно распространять эту статью любыми способами целиком вместе с этим блоком и действующей гиперссылкой на сайт finware.ru.
———————————————