Приблизительное время чтения: 18 минут
Измерение периодов цикла позволяет корректировать индикаторы, чтобы они адаптировались к текущим рыночным условиям. Вот как.
Если вы хотите, чтобы ваши индикаторы и стратегии адаптировались к текущим рыночным условиям, вам необходимо сначала измерить периоды циклов, которые присутствуют в данных. Если вам известен доминирующий цикл, вы можете использовать эту информацию для динамической корректировки своих вычислений. Например, вы можете установить период наблюдения за индексом относительной силы (RSI) равным половине доминирующего цикла. Ранее я уже описывал практический способ использования прямого преобразования Фурье (Discrete Fourier Transform, DFT, русск. — ДПФ) для оценки рыночного спектра. Но ДПФ — не единственный способ оценить рыночный спектр.
ИСПОЛЬЗОВАНИЕ ПОЛОСОВЫХ ФИЛЬТРОВ
В этой статье я описываю способ использования полосовых фильтров для оценки спектра. Полосовые фильтры выгодны тем, что можно управлять избирательностью и переходной характеристикой фильтра. Это важно, поскольку не все фильтры подходят для торговли, так как фильтры вызывают запаздывание на выходе и, следовательно, приводят к задержке в принятии торговых решений. В целом, чем сложнее фильтр, тем больше запаздывание. Простой двухполюсный полосовой фильтр хорош тем, что он не дает запаздывания на выходе при стабильном входном сигнале на частоте, на которую настроен полосовой фильтр.
Для начала давайте разберемся в некоторых основах работы полосовых фильтров. Импульсная характеристика фильтра показана на рисунке 1. Это означает, что при подаче на вход фильтра сигналов равной амплитуды на всех относительных частотах фильтр отбрасывает частотные составляющие, которые как выше, так и ниже настроенной частоты фильтра. Амплитуды частотных составляющих на выходе фильтра формируются фильтром. Область относительных частот от -0,5 до +0,5 является полосой пропускания полосового фильтра, поскольку большая часть энергии, проходящей через фильтр, попадает в этот диапазон.
С точки зрения торговли, отбрасывание более низких и более высоких частотных составляющих имеет два эффекта. Во-первых, более низкие частоты (с большей длиной волны) содержат информацию о тренде во входном сигнале, поэтому их отклонение детерминирует данные. Во-вторых, более высокие частоты содержат быстрые изменения в зависимости от времени, поэтому их отклонение выполняет операцию сглаживания данных. Что может быть лучше фильтра, который не имеет запаздывания, отбрасывает данные, а также сглаживает их? Большое «если» в этой ситуации заключается в том, что все это верно только в том случае, если фильтр настроен на устойчивый доминирующий цикл в данных. Поскольку полосовой фильтр обладает частотной избирательностью, мы можем воспользоваться этим фактом, чтобы определить доминирующий цикл в данных. Как это сделать, я опишу позже.
Inputs:
Price((H+L)/2), ShowDC(False);
Vars:
delta(0.1),
gamma(0),
alpha(0),
beta(0),
N(0),
Period(0), MaxAmpl(0), Num(0),
Denom(0),
DC(0),
DomCyc(0), Color1(0), Color2(0), alpha1(0), HP(0),
SmoothHP(0);
Arrays:
I[50](0),
OldI[50](0),
OlderI[50](0),
Q[50](0),
OldQ[50](0),
OlderQ[50](0),
Real[50](0),
OldReal[50](0), OlderReal[50](0), Imag[50](0),
OldImag[50](0), OlderImag[50](0), Ampl[50](0),
OldAmpl[50](0),
DB[50](0);
alpha1 = (1 — Sine (360 / 40)) / Cosine(360 / 40);
HP = .5*(1 + alpha1)*(Price — Price[1]) + alpha1*HP[1]; SmoothHP = (HP + 2*HP[1] + 3*HP[2] + 3*HP[3] + 2*HP[4] + HP[5]) / 12;
IF CurrentBar < 7 Then SmoothHP = Price — Price[1]; IF CurrentBar = 1 THEN SmoothHP = 0;
delta = -.015*CurrentBar + .5; If delta < .15 then delta = .15;
If CurrentBar > 6 Then Begin For N = 8 to 50 Begin
beta = Cosine(360 / N);
gamma = 1 / Cosine(720*delta / N);
alpha = gamma — SquareRoot(gamma*gamma — 1); Q[N] = (N / 6.283185)*(SmoothHP —
SmoothHP[1]);
I[N] = SmoothHP;
Real[N] = .5*(1 — alpha)*(I[N] — OlderI[N]) + beta*(1
+ alpha)*OldReal[N] — alpha*OlderReal[N];
Imag[N] = .5*(1 — alpha)*(Q[N] — OlderQ[N]) + beta*(1 + alpha)*OldImag[N] — alpha*OlderImag[N];
Ampl[N] = (Real[N]*Real[N] + Imag[N]*Imag[N]);
End; End;
For N = 8 to 50 Begin OlderI[N] = OldI[N]; OldI[N] = I[N];
OlderQ[N] = OldQ[N]; OldQ[N] = Q[N];
OlderReal[N] = OldReal[N]; OldReal[N] = Real[N]; OlderImag[N] = OldImag[N]; OldImag[N] = Imag[N]; OldAmpl[N] = Ampl[N];
End;
MaxAmpl = Ampl[10]; For N = 8 to 50 Begin
If Ampl[N] > MaxAmpl then MaxAmpl = Ampl[N]; End;
For N = 8 to 50 Begin
IF MaxAmpl <> 0 AND (Ampl[N] / MaxAmpl) > 0 THEN DB[N] =
-10*Log(.01 / (1 — .99*Ampl[N] / MaxAmpl)) / Log(10); If DB[N] > 20 then DB[N] = 20;
End; Num = 0;
Denom = 0;
For N = 8 to 50 Begin
If DB[N] <= 3 Then Begin
Num = Num + N*(20 — DB[N]);
Denom = Denom + (20 — DB[N]);
End;
If Denom <> 0 Then DC = Num / Denom; End;
DomCyc = Median(DC, 10);
If ShowDC = True Then Plot1(DomCyc, “DC”, RGB(0, 0, 255), 0, 2);
For N = 8 to 50 Begin
IF DB[N] <= 10 THEN Begin
Color1 = 255;
Color2 = 255*(1 — DB[N] / 10); END;
IF DB[N] > 10 THEN Begin Color1 = 255*(2 — DB[N] / 10);
Color2 = 0; END;
If N = 8 Then Plot8(N, “S8”, RGB(Color1, Color2, 0),0,5);
If N = 9 Then Plot9(N, “S9”, RGB(Color1, Color2, 0),0,5);
If N = 10 Then Plot10(N, “S10”, RGB(Color1, Color2, 0),0,5);
If N = 11 Then Plot11(N, “S11”, RGB(Color1, Color2, 0),0,5);
If N = 12 Then Plot12(N, “S12”, RGB(Color1, Color2, 0),0,5);
If N = 13 Then Plot13(N, “S13”, RGB(Color1, Color2, 0),0,5);
If N = 14 Then Plot14(N, “S14”, RGB(Color1, Color2, 0),0,5);
If N = 15 Then Plot15(N, “S15”, RGB(Color1, Color2, 0),0,5);
If N = 16 Then Plot16(N, “S16”, RGB(Color1, Color2, 0),0,5);
If N = 17 Then Plot17(N, “S17”, RGB(Color1, Color2, 0),0,5);
If N = 18 Then Plot18(N, “S18”, RGB(Color1, Color2, 0),0,5);
If N = 19 Then Plot19(N, “S19”, RGB(Color1, Color2, 0),0,5);
If N = 20 Then Plot20(N, “S20”, RGB(Color1, Color2, 0),0,5);
If N = 21 Then Plot21(N, “S21”, RGB(Color1, Color2, 0),0,5);
If N = 22 Then Plot22(N, “S22”, RGB(Color1, Color2, 0),0,5);
If N = 23 Then Plot23(N, “S23”, RGB(Color1, Color2, 0),0,5);
If N = 24 Then Plot24(N, “S24”, RGB(Color1, Color2, 0),0,5);
If N = 25 Then Plot25(N, “S25”, RGB(Color1, Color2, 0),0,5);
If N = 26 Then Plot26(N, “S26”, RGB(Color1, Color2, 0),0,5);
If N = 27 Then Plot27(N, “S27”, RGB(Color1, Color2, 0),0,5);
If N = 28 Then Plot28(N, “S28”, RGB(Color1, Color2, 0),0,5);
If N = 29 Then Plot29(N, “S29”, RGB(Color1, Color2, 0),0,5);
If N = 30 Then Plot30(N, “S30”, RGB(Color1, Color2, 0),0,5);
If N = 31 Then Plot31(N, “S31”, RGB(Color1, Color2, 0),0,5);
If N = 32 Then Plot32(N, “S32”, RGB(Color1, Color2, 0),0,5);
If N = 33 Then Plot33(N, “S33”, RGB(Color1, Color2, 0),0,5);
If N = 34 Then Plot34(N, “S34”, RGB(Color1, Color2, 0),0,5);
If N = 35 Then Plot35(N, “S35”, RGB(Color1, Color2, 0),0,5);
If N = 36 Then Plot36(N, “S36”, RGB(Color1, Color2, 0),0,5);
If N = 37 Then Plot37(N, “S37”, RGB(Color1, Color2, 0),0,5);
If N = 38 Then Plot38(N, “S38”, RGB(Color1, Color2, 0),0,5);
If N = 39 Then Plot39(N, “S39”, RGB(Color1, Color2, 0),0,5);
If N = 40 Then Plot40(N, “S40”, RGB(Color1, Color2, 0),0,5);
If N = 41 Then Plot41(N, “S41”, RGB(Color1, Color2, 0),0,5);
If N = 42 Then Plot42(N, “S42”, RGB(Color1, Color2, 0),0,5);
If N = 43 Then Plot43(N, “S43”, RGB(Color1, Color2, 0),0,5);
If N = 44 Then Plot44(N, “S44”, RGB(Color1, Color2, 0),0,5);
If N = 45 Then Plot45(N, “S45”, RGB(Color1, Color2, 0),0,5);
If N = 46 Then Plot46(N, “S46”, RGB(Color1, Color2, 0),0,5);
If N = 47 Then Plot47(N, “S47”, RGB(Color1, Color2, 0),0,5);
If N = 48 Then Plot48(N, “S48”, RGB(Color1, Color2, 0),0,5);
If N = 49 Then Plot49(N, “S49”, RGB(Color1, Color2, 0),0,5);
If N = 50 Then Plot50(N, “S50”, RGB(Color1, Color2, 0),0,5);
End;
РЕГУЛИРОВКА ПОЛОСЫ ПРОПУСКАНИЯ
Полосовой фильтр может иметь регулируемую полосу пропускания. На рисунке 2 красным цветом показан оригинальный фильтр с полосой пропускания относительных частот от -0,5 до +0,5, а синим — фильтр с гораздо большей избирательностью, то есть полоса пропускания более узкая. В принципе, мы можем сделать полосу пропускания полосового фильтра произвольно узкой, но мы не хотим делать этого в торговле, потому что сужение полосы пропускания негативно влияет на переходную характеристику фильтра.
Например, колокол спроектирован как высокоселективный полосовой фильтр. Когда хлопушка ударяет в колокол, он продолжает звонить на своей настроенной частоте. Таким образом, мы слышим реакцию на событие, но само событие теряется. Кроме того, звон продолжается еще долго после того, как первоначальное событие произошло и исчезло.
Любой высокоизбирательный фильтр имеет такое явление, и этот звон не помогает в интерпретации рыночных действий. Да, мы хотим извлечь из данных информацию о доминирующем цикле, но мы также надеемся, что реакция преходящего фильтра на внезапное изменение быстро угаснет. Единственный способ добиться этого — расширить полосу пропускания полосового фильтра.
Работа с откликами в большинстве торговых данных не представляет собой большой проблемы, поскольку доминирующие циклы имеют тенденцию дрейфовать со временем, а не перескакивать с одного периода цикла на другой. С другой стороны, если вы используете внутридневные данные, вам следует опасаться открытия гэпов, поскольку они представляют собой сильные отклики, которые могут исказить анализ на основе фильтра.
По сути, мы хотим воспользоваться селективностью полосового фильтра, чтобы выявить доминирующий цикл в данных. Найдя этот цикл, мы можем динамически настраивать любой из множества показателей.
На рисунке 3 показана основная концепция того, как мы это делаем. Если входной сигнал попадает в полосу пропускания фильтра А, то выход фильтра А будет иметь большую амплитуду, чем выход фильтра В. И наоборот, если входной сигнал попадает в полосу пропускания фильтра В, то выход фильтра В будет иметь большую амплитуду, чем выход фильтра А. Таким образом, для измерения спектра входного сигнала нам нужно создать последовательный банк перекрывающихся фильтров, как показано на рисунке 4, и измерить амплитуду сигнала на выходе каждого фильтра.
ИЗМЕРЕНИЕ АМПЛИТУДЫ
Поскольку полоса пропускания каждого фильтра относительно узкая, сигнал на каждом выходе можно охарактеризовать как синусоиду с медленно меняющейся фазой. Из курса вычислений вы можете вспомнить, что:
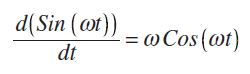
Поэтому умножение скорости изменения выходного сигнала каждого фильтра на Period/2π приводит к тому, что на выходе каждого фильтра также возникает косинусоидальная волна. И синусоидальная, и косинусоидальная волны имеют обобщенную амплитуду A. Далее, из знакомого тригонометрического тождества:
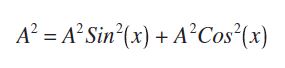
мы получаем показатель амплитуды сигнала на выходе каждого фильтра путем возведения в квадрат и сложения синусоиды и косинусоиды. Вот, собственно, и все, что нужно для получения спектра рыночных данных.
Inputs:
Price((H+L)/2);
Vars:
delta(0.1),
gamma(0),
alpha(0),
beta(0),
N(0),
Period(0), MaxAmpl(0), Num(0),
Denom(0),
DC(0),
DomCyc(0), Color1(0), Color2(0), alpha1(0), HP(0),
SmoothHP(0);
Arrays:
I[50](0),
OldI[50](0),
OlderI[50](0),
Q[50](0),
OldQ[50](0),
OlderQ[50](0),
Real[50](0),
OldReal[50](0), OlderReal[50](0), Imag[50](0),
OldImag[50](0), OlderImag[50](0), Ampl[50](0),
OldAmpl[50](0),
DB[50](0);
alpha1 = (1 — Sine (360 / 40)) / Cosine(360 / 40);
HP = .5*(1 + alpha1)*(Price — Price[1]) + alpha1*HP[1]; SmoothHP = (HP + 2*HP[1] + 3*HP[2] + 3*HP[3] + 2*HP[4] + HP[5]) / 12;
IF CurrentBar < 7 Then SmoothHP = Price — Price[1]; IF CurrentBar = 1 THEN SmoothHP = 0;
delta = -.015*CurrentBar + .5; If delta < .15 then delta = .15;
If CurrentBar > 6 Then Begin For N = 8 to 50 Begin
beta = Cosine(360 / N);
gamma = 1 / Cosine(720*delta / N);
alpha = gamma — SquareRoot(gamma*gamma — 1);
Q[N] = (N / 6.283185)(SmoothHP — SmoothHP[1]); I[N] = SmoothHP; Real[N] = .5(1 — alpha)(I[N] — OlderI[N]) + beta(1 +
alpha)OldReal[N] — alphaOlderReal[N];
Imag[N] = .5(1 — alpha)(Q[N] — OlderQ[N]) + beta*(1
alpha)OldImag[N] — alphaOlderImag[N];
Ampl[N] = (Real[N]Real[N] + Imag[N]Imag[N]);
End;
End;
For N = 8 to 50 Begin
OlderI[N] = OldI[N];
OldI[N] = I[N];
OlderQ[N] = OldQ[N];
OldQ[N] = Q[N];
OlderReal[N] = OldReal[N];
OldReal[N] = Real[N];
OlderImag[N] = OldImag[N];
OldImag[N] = Imag[N];
OldAmpl[N] = Ampl[N];
End;
MaxAmpl = Ampl[10];
For N = 8 to 50 Begin
If Ampl[N] > MaxAmpl then MaxAmpl = Ampl[N];
End;
For N = 8 to 50 Begin
IF MaxAmpl <> 0 AND (Ampl[N] / MaxAmpl) > 0 THEN DB[N]
= -10Log(.01 / (1 — .99Ampl[N] / MaxAmpl)) / Log(10);
If DB[N] > 20 then DB[N] = 20;
End;
Num = 0;
Denom = 0;
For N = 10 to 50 Begin
If DB[N] <= 3 Then Begin
Num = Num + N(20 — DB[N]); Denom = Denom + (20 — DB[N]); End; If Denom <> 0 Then DC = Num / Denom; End; DomCyc = Median(DC, 10); If DomCyc < 8 Then DomCyc = 20; beta = Cosine(360 / DomCyc); gamma = 1 / Cosine(720delta / DomCyc);
alpha = gamma — SquareRoot(gammagamma — 1); Value1 = .5(1 — alpha)(SmoothHP — SmoothHP[1]) + beta(1
alpha)Value1[1] — alphaValue1[2];
Value2 = (DomCyc / 6.28)*(Value1 — Value1[1]);
Plot1(Value1, “Sine”, Red, default, 2);
Plot2(Value2, “Cosine”, Cyan, default, 2);
Некоторые детали проще объяснить на примере кода на языке EasyLanguage в первой вкладке, «Код на языке EasyLanguage для отображения спектра, полученного из банка фильтров». При переводе кода на другие языки следует обратить внимание на несколько особенностей. Во-первых, весь код заполняется для каждого бара, и значения переменных сохраняются от бара к бару. Однако значения массивов не индексируются автоматически для каждого ценового бара. Во-вторых, EasyLanguage использует в качестве аргументов тригонометрической функции градусы, а не радианы. Наконец, обозначение Price[1] — то есть с квадратными скобками — означает значение цены на один бар назад по отношению к переменным. Нотация с квадратными скобками также указывает на позицию внутри массива.
В индикаторе всего два входа. Один из них — цена, и я привык использовать среднее значение максимума и минимума каждого бара. Использование цен закрытия — это нормально. Другой вход — это решение о том, показывать ли на дисплее доминирующий цикл (ShowDC). Как обычно, определяются и инициализируются переменные и массивы. Первым вычислением является 40-барный фильтр высоких частот, используемый для детрендинга данных. Затем детрендированные данные сглаживаются шестичастотным фильтром с конечным импульсным откликом (FIR) с малым запаздыванием.
Дельта — это полуширина полосы пропускания каждого полосового фильтра относительно его центральной частоты. Например, если дельта = 0,15, то фильтр с центром на 20-барном цикле будет иметь полосу пропускания от 17-барного до 23-барного цикла. Дельта начинается со значения 0,5, чтобы минимизировать переходный процесс при запуске. Дельта постепенно уменьшается и достигает значения 0,15 примерно через 50 баров в начале.
Следующий раздел кода фактически вычисляет полосовые фильтры в центрах каналов от восьми баров до 50 баров с шагом в один бар. Я использовал подход, при котором сглаженные и детрендированные данные используются в качестве переменной I[N] (обозначение для синфазной составляющей), а данные о скорости изменения — в качестве переменной Q[N] (обозначение для квадратурной составляющей) перед применением полосового фильтра. Оба компонента фильтруются в идентичных канальных полосовых фильтрах, поэтому они имеют одинаковые задержки и фазовые сдвиги. Обе компоненты возводятся в квадрат и суммируются, чтобы вычислить мгновенную амплитуду сигнала на выходе каждого канала фильтра.
Затем код находит сигнал с наибольшей амплитудой для целей нормализации. Затем нормализованная амплитуда преобразуется в децибелы одновременно с применением нелинейного преобразования для повышения резкости изображения. Нелинейное преобразование было описано в моей статье о практическом применении ДПФ для торговли в январском номере журнала STOCKS & COMMODITIES за 2006 год. Затем доминирующий цикл вычисляется как центр тяжести тех каналов, амплитуда которых больше -3 дБ относительно канала с наибольшей амплитудой. Использование центра тяжести приводит к более гладкому результату, чем просто выбор канала с наибольшей амплитудой.
Затем амплитуды каналов преобразуются в цветовое значение. Если амплитуда находится в диапазоне от нуля до 10 дБ, цвет переходит от желтого к красному, а если амплитуда находится в диапазоне от 10 до 20 дБ, цвет переходит от красного к черному. Наконец, выход каждого канала отображается в виде окрашенной линии, вертикальное положение которой на подграфе соответствует амплитуде сигнала на выходе этого канала. Таким образом, измеренный спектр может быть построен синхронно с гистограммой (рис. 5).
ПРИМЕНЕНИЕ
В качестве интересного примера я выбрал 1000-тиковый график дневной сессии фьючерсного контракта S&P emini 2 августа 2007 года. Этот график представляет собой мимолетный интерес, потому что график эквитик имеет нелинейную горизонтальную ось времени, поскольку каждый бар содержит ровно 1 000 тиков. Таким образом, график сам по себе является индикатором денежного потока или, по крайней мере, потока активности. График показывает относительно постоянный период цикла между 30 и 35 барами, с небольшими колебаниями в конце утра.
Возможно, более важный вопрос — «Так чем же полезна эта информация?». Во вкладке «Код EasyLanguage для обходного фильтра, настроенного на доминирующий цикл» я показываю код, в котором измеренный доминирующий цикл используется для настройки обходного фильтра. Код точно такой же, как и для вычисления спектра, за исключением того, что измеренный доминирующий цикл используется для настройки полосового фильтра. Синусоидальные и косинусоидальные выходы этого фильтра строятся так, чтобы пересечения можно было использовать в качестве сигналов покупки и продажи.
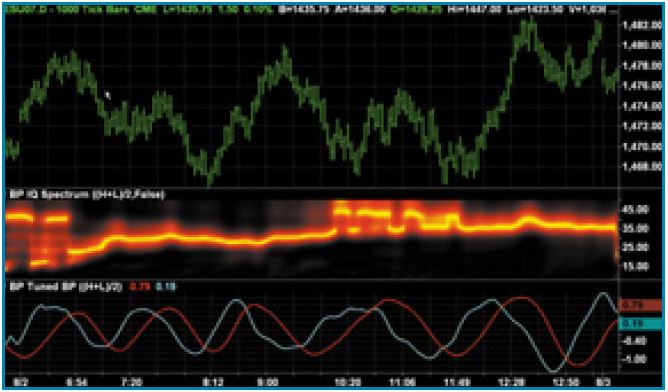
Поскольку доступны как синфазные, так и квадратурные компоненты, можно легко выполнить дополнительную настройку для изменения фазы отображаемого индикатора. На рисунке 6 показан отклик полосового фильтра, настроенного на доминирующий цикл, для того же графика Equitick. Синусоидальная составляющая показана красным цветом, а косинусоидальная — голубым. Синусоидальная составляющая явно является сглаженной копией ценовых баров, а косинусоидальная составляющая является опережающей функцией — иногда даже слишком опережающей — синусоидальной составляющей.
НЕ ОДИН СПОСОБ
Существует не один способ снять шкуру с кошки — не один способ измерить спектр и определить доминирующий цикл в рыночных данных.
Об Авторе:
Джон Эйлерс — пионер в области использования циклов и методов DSP в техническом анализе. Он является автором программы MESA8, а также сайтов www.eminiz.com и www.indicez.com, посвященных трейдингу.
ПРЕДЛАГАЕМАЯ ЛИТЕРАТУРА:
Эйлерс, Джон [2007]. «Преобразование Фурье для трейдеров», Technical Analysis of STOCKS & COMMODITIES, том 25: Январь.
[2006]. «Индикатор швейцарского армейского ножа», Technical Analysis of STOCKS & COMMODITIES, том 24: январь.
———————————————————
Переведено специально для сайта Finware Technologies, www.finware.ru
Вы можете свободно распространять эту статью любыми способами целиком вместе с этим блоком и действующей гиперссылкой на сайт finware.ru.
———————————————————

Оставьте первый комментарий