Адаптивная скользящая средняя для свинг-трейдинга

Приблизительное время чтения: 10 минут

В данной статье мы представляем новую адаптивную скользящую среднюю, которая отличается быстродействием, плавностью и надежностью.

В этой статье я предложу новую адаптивную скользящую среднюю (AMA). Она автоматически настраивает свои параметры в зависимости от волатильности рынка, внимательно следит за ценой при трендовом движении, оставаясь ровной в зонах заторов. Новая АМА хорошо подходит для свинг-трейдинга.

Данная работа является частью усилий по количественной оценке инновационного метода торговли, разработанного великим китайским трейдером, известным под именем:

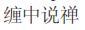
(в переводе с китайского «дзен в запутанности») и сейчас уже хорошо известного в Западных трейдерских кругах под именем Chan Lun (Чан Лун). Значение его вклада в область технического анализа велико и сравнимо со значением изобретения перехода к графику японских свечей от обычной, простой гистограммы.

ВВЕДЕНИЕ

Технические индикаторы предоставляют трейдерам одну или несколько из следующих идей о движении цены: направление, импульс и вероятная граница.

Скользящие средние (MA — «moving averages») относятся к категории индикаторов, которые могут помочь в решении всех трех этих задач. Одна из функций МА — отфильтровать шум и выявить основную тенденцию.

Другая функция заключается в прогнозировании будущего движения и определении уровня поддержки/сопротивления. Однако МА имеют и один существенный недостаток: они вносят запаздывание.

Было разработано множество версий скользящих средних, призванных обеспечить быстрый отклик, уменьшить запаздывание и максимально отфильтровать шум. Их характеристики зависят от алгоритма построения и периода обратного хода. Чтобы соответствовать своему стилю торговли, трейдеры идут на компромисс между быстротой отклика и «вихрями» при выборе конкретной МА и периода возврата.

Рынок постоянно меняется. Использование фиксированного периода возврата, скорее всего, не принесет успеха.

Желательно, чтобы МА менялась в зависимости от рыночных условий, чтобы обеспечить быстроту реакции и в то же время минимизировать «биения». Адаптивная скользящая средняя Перри Кауфмана, впервые описанная в его книге «Разумный трейдинг» (1995 г.), является отличным примером того, как AMA может самонастраиваться, адаптируясь к изменяющимся условиям.
В данной статье представлена новая схема адаптивной скользящей средней, которая является отзывчивой, плавной и надежной.

ПРИНЦИПЫ ПОСТРОЕНИЯ СКОЛЬЗЯЩИХ СРЕДНИХ

Адаптивные скользящие средние могут быть рассчитаны прогрессивно следующим образом:

AMA = a * Close + (1 — a) * AMA(1) (уравнение 1), где:

a = коэффициент сглаживания от 0 до 1, определяемый периодом обратного хода
Close = закрытие бара
AMA(1) = значение AMA предыдущего бара.

Методика Кауфмана заключается в корректировке коэффициента сглаживания среднего в зависимости от соотношения направления рынка и волатильности. Он использует переменную, которую называет коэффициентом эффективности (ER):

Коэффициент эффективности = Направление / Волатильность (уравнение 2), где:
Направление: Close — Close(n)
Волатильность: Сумма (абсолютное значение(close — close(1)), n).

Более подробно с работой Кауфмана можно ознакомиться в его книге, упомянутой выше и приведенной в конце раздела «Дополнительная литература».

НОВАЯ АДАПТИВНАЯ СКОЛЬЗЯЩАЯ СРЕДНЯЯ

Из уравнения 1 видно, что эффективность АМА зависит от того, как рассчитывается коэффициент сглаживания. Коэффициент эффективности Кауфмана наводит меня на мысль оценить эффективность с точки зрения соотношения результата и усилий:

RE = Результат / Усилия (уравнение 3)
Вопрос в том, как логично и разумно определить результат и усилия.

Усилия

Цена перемещается из точки, где она находилась n периодов назад, в текущую точку. Во время этого путешествия она двигается вверх и вниз от бара к бару. Вместо того чтобы называть это движение «шумом», мы можем считать его «усилием», поскольку быки и медведи сражаются на каждом баре, чтобы в конце концов достичь того уровня, на котором она находится сейчас.

Адаптивная скользящая средняя, которую я предлагаю здесь, показывает, что она чутко реагирует на изменения цены даже на быстро меняющемся рынке.

Поскольку движение непрерывно, диапазон каждого бара можно определить с помощью истинного диапазона Уайлдера (TR). Суммируя отдельные истинные диапазоны за n периодов, мы получим общий диапазон, следовательно:

Усилие = Сумма (TR, n) (уравнение 4)

Результат

Обычно в качестве результата рассматривается смещение цены между текущим моментом и началом периода наблюдения n (здесь нас интересует только абсолютное значение, чтобы a всегда было не меньше нуля):

Результат = Абсолютное значение закрытия -Close(n периодов назад) (уравнение 5)

Это определение рассматривает только результат и игнорирует детали внутри этого процесса. А что если поступить наоборот и определить результат, исходя не из конечного изменения, а из процесса? Будет ли это иметь смысл?
В рассматриваемом периоде цена движется от начальной цены O до конечной цены C. В процессе движения она достигла наивысшего значения H и наименьшего значения L. H было достигнуто быками, а L — медведями. Быки всегда стремятся подняться выше, а медведи — опуститься ниже. В любом случае они преследуют одну и ту же цель: расширить диапазон. O и C — это всего лишь две точки наблюдения за ходом битвы, которые по случайности являются началом и концом окна наблюдения.

Поэтому разумно также определить результат как максимальный диапазон движения:

Результат = Наибольшая цена за n период — Самая низкая цена n-го периода (уравнение 6)

Подставив в формулу 3 уравнение 5 или 6, можно рассчитать коэффициент сглаживания всего в одной строке кода:

a = Result / Sum(TR, n) (уравнение 7)

Так как диапазон цен всегда не превышает суммарную поездку, a находится в пределах от 0 до 1, что является обязательным условием для работы уравнения 1.

ОБСУЖДЕНИЕ:

Если цена находится в одностороннем трендовом движении, как вверх, так и вниз, то максимальный диапазон практически совпадает с суммой диапазонов отдельных баров, a будет около 1, а 1-a — около нуля. Из уравнения 1 следует, что новое значение АМА будет в основном определяться текущей ценой. Поэтому в условиях тренда кривая АМА будет четко следовать за ценой.
В зонах скоплений, где диапазон мал, a также мало. Из уравнения 1 следует, что текущая цена будет вносить незначительный вклад в новое значение AMA. АМА будет находиться вблизи своего прежнего уровня. Кривая в этих ситуациях относительно плоская.

Именно такого поведения мы ожидаем от АМА.

AMA автоматически подстраивает свои параметры в соответствии с волатильностью рынка, внимательно отслеживая цену в трендовом движении и оставаясь ровным в зонах перегруженности.

ДЕМОНСТРАЦИЯ:

Обе схемы АМА, приведенные в уравнениях 5 и 6, показаны на рис. 1 для индекса австралийского фондового рынка (XJO) с апреля 2022 года по начало декабря 2022 года. Движение цены разбито на восемь участков. Период обратного хода равен 30. В периоды быстрых движений A, C, E и H АМА отслеживают движение цены точно, без размаха. На участке F метод смещения цены пытался угнаться за откатом, в то время как метод максимального диапазона сохранял свое направление. Участок B — это откат от быстрого движения вниз на участке A. АМА явно испытывают трудности с разворотом после резкого движения в противоположном направлении. В этот период, а также в периоды перегрузок D и G они идут флэтом.

Интересно отметить, что на некоторых участках схема смещения цен работает лучше, в то время как на других участках лучше работает метод максимального диапазона. В целом метод максимального диапазона имеет меньшие колебания и более жестко придерживается цены. Это может быть несколько выгодно для разработчиков торговых систем. Однако он страдает от более сильных колебаний. Схема смещения цены будет использоваться в последующих примерах.

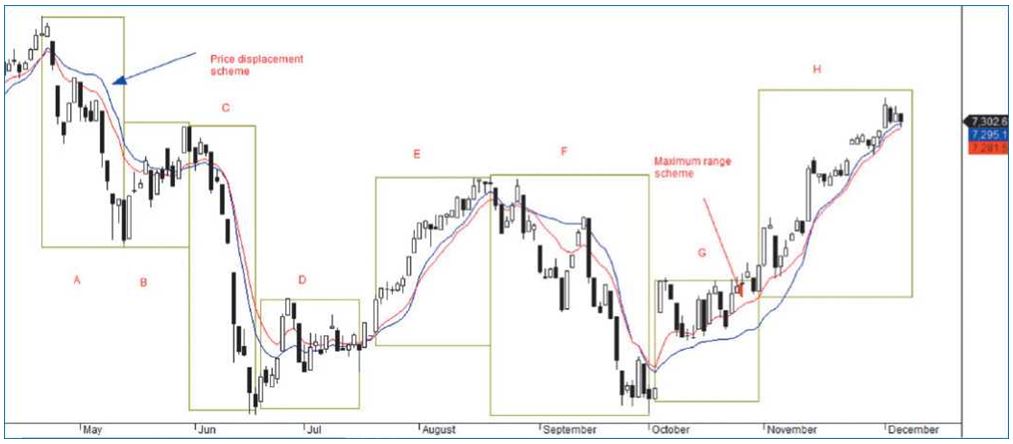
На рис. 2 показано сравнение АМА с простой скользящей средней (SMA) и экспоненциальной скользящей средней (EMA) за тот же период. Очевидно, что в условиях тренда новая АМА более отзывчива, чем обе эти модели. Она улавливает больше трендовых движений, чем две другие МА, с меньшим количеством виляний, что делает ее лучшим выбором для определения тренда и в качестве трейлинг-стопа при свинговой торговле.

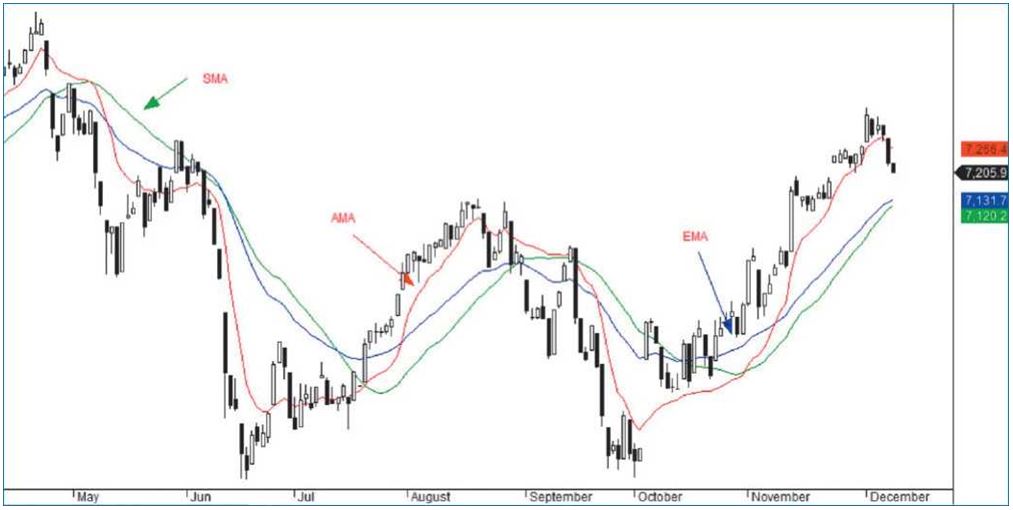
На рис. 3 показаны АМА с двумя более короткопериодными ЕМА — 10 и 20. Интересно, что в периоды быстрого движения АМА реагирует даже быстрее, чем 10-периодная ЕМА, а в периоды заторов — медленнее, чем 20-периодная ЕМА, что уменьшает «вип-пики», характерные для большинства короткопериодных скользящих средних.

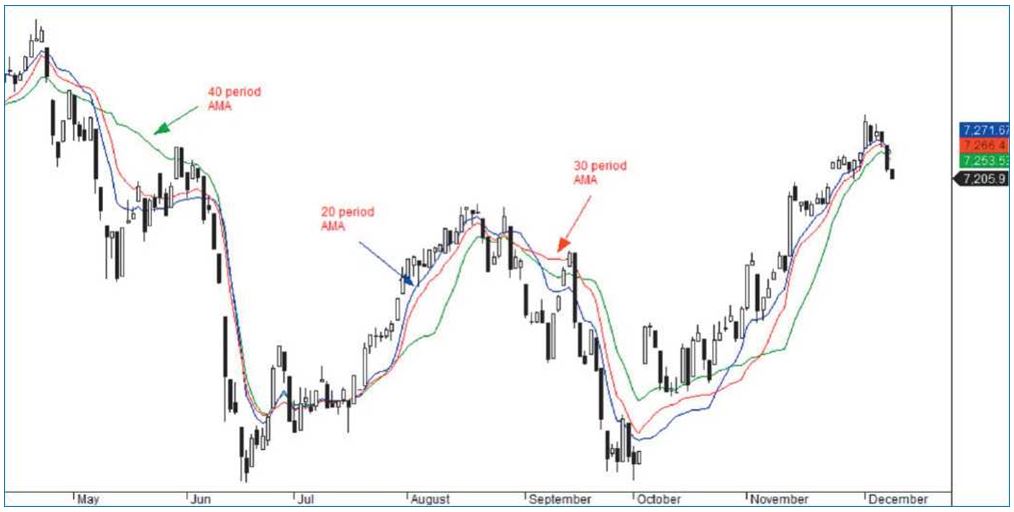
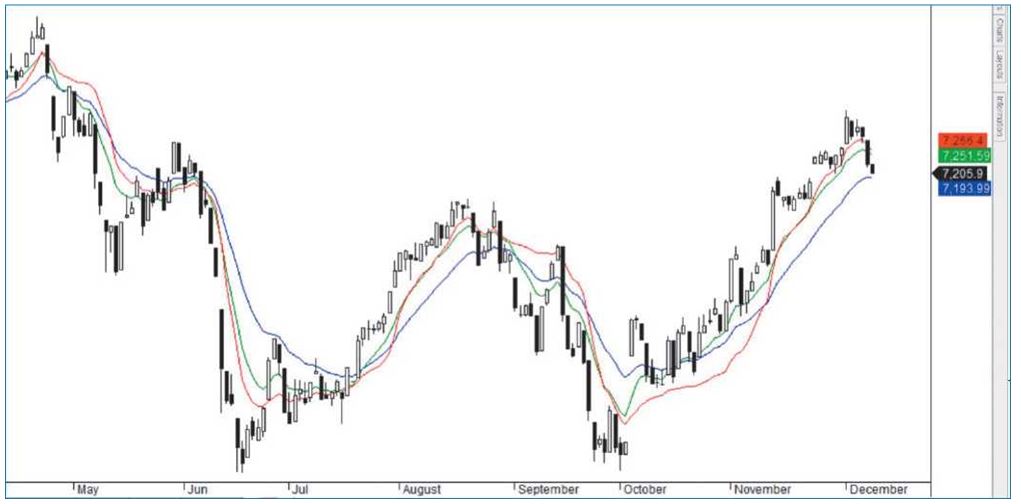
На рис. 4 показана АМА трех различных периодов — 20, 30 и 40. В периоды тренда все три АМА внимательно следят за ценой. Только в периоды заторов они немного расходятся. Это желательное поведение, так как оно означает, что АМА не очень чувствительна к выбору параметров в диапазоне.

ЗАКЛЮЧЕНИЕ

Предложенная мною адаптивная скользящая средняя показывает, что она чутко реагирует на изменения цены даже на быстро меняющемся рынке. Примеры приведены только для XJO, но АМА хорошо работает и для других инструментов. Она достаточно плавная и толерантная к изменениям параметров. Алгоритм очень прост и состоит всего из одной строки кода, тем не менее, его производительность радует.

Об Авторе: Скот Конг (Scott Cong) — инженер на пенсии. До переезда в Австралию в 1990 г. он преподавал электротехнику в одном из ведущих университетов Китая. В течение 30 лет он является частным трейдером. За время этого долгого и порой мучительного пути он понял, что для достижения успеха на рынке трейдеру необходимо хорошо изучить самого себя.

———————————————————
Переведено для сайта Finware Technologies, www.finware.ru
Вы можете свободно распространять эту статью любыми способами целиком вместе с этим блоком и действующей гиперссылкой на сайт finware.ru.
———————————————————

ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА:

1. Kaufman, Perry J. [1995]. Smarter Trading, McGraw- Hill.
2. Hartle, Thom [1995]. «Perry Kaufman On Market Analysis», интервью, Technical Analysis of STOCKS & COMMODITIES, Volume 13: June.
3. Метод ЧанЛун
4. Оригинальный текст Автора — «Техническая теория фондового рынка «Дзен в запутанности» (на китайском языке)

Видео-интервью с Перри Кауфманом:

Поделитесь этим материалом с друзьями:

Вам также может быть интересно:

1. Определение разворотных точек с помощью Метода ЧанЛун (ChanLun)
2. Стоит ли пользоваться индикаторами технического анализа?
3. Индикаторы тренда и компоненты цены
4. Идентификация трендов на форексе
5. Принципы торговли на Скользящих средних
6. Скользящие средние
7. Новый адаптивный метод следования за тенденцией и рыночными циклами