Броуновское движение, как модель для прогнозирования финансовых активов

Рис.5

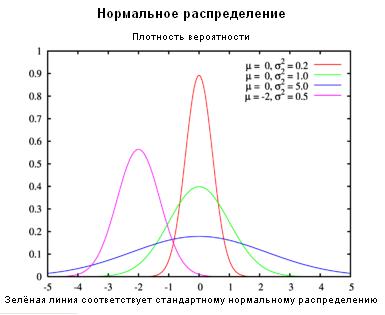
Нормальное распределение, также называемое распределением Гаусса, — распределение вероятностей, которое играет важнейшую роль во многих областях знаний, особенно в физике. Физическая величина подчиняется нормальному распределению, когда она подвержена влиянию огромного числа случайных помех. Ясно, что такая ситуация крайне распространена, поэтому можно сказать, что из всех распределений, в природе чаще всего встречается именно нормальное распределение — отсюда и произошло одно из его названий.

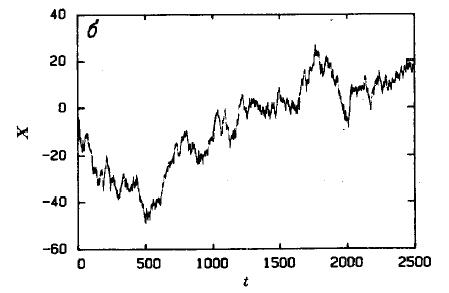
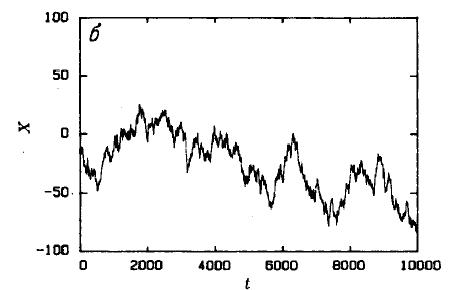
На рис.6 изображена более реалистичная модель, которая соответствует поведению финансовых активов.

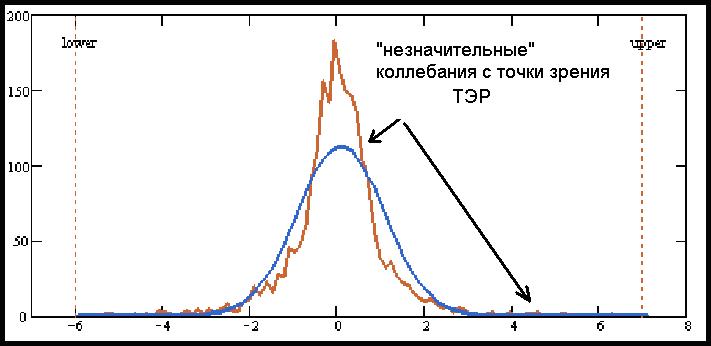
Как же может быть так, что цены все же являются броуновским движением?

Для того, что бы ответить на поставленную задачу нам необходимо познакомиться с показателем Херста.

Гарольд Эдвин Херст (1880-1978) – английский физик, ставший великим «нилологом» и заслуживший прозвище Абу Нил, «отец Нила». Наука обязана ему одним замечательным статистическим изобретением и одним замечательным эмпирическим (практическим) открытием, которые связаны с идеей об измерении интенсивности некоторой хроники (событий) стремиться быть циклической, но НЕ ПЕРИОДИЧЕСКОЙ, — поведение, представляющее собой один из аспектов долговременной статистической зависимости прошлого от будущего.

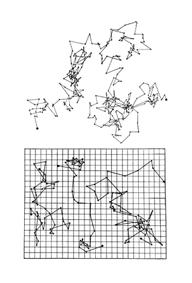
Здесь мы вспомним про нашу частицу, движение которой представляется броуновским. Мы помним, что координаты частицы в одном промежутке времени подобны ее же координатам в другом промежутке, однако появление циклов носит не периодический характер, т.е мы не знаем дальнейшее положение частицы через определенное время t.

Херст, не отдавая себе в этом отчета, ввел новую статистическую технику, основанную на выражении R(t, d)/S(t, d). Этот метод был назван R/S анализ. В данной статье мы не будем разбирать этот метод, поскольку он не имеет прямого отношения к нашей с вами задаче, для тех кому интересно применение данного анализа к биржевым ценам могут прочесть Эдгара Петерса «Фрактальный анализ финансовых рынков». Нас же больше интересует, результат который получил Херст используя данный метод.

Рис.7

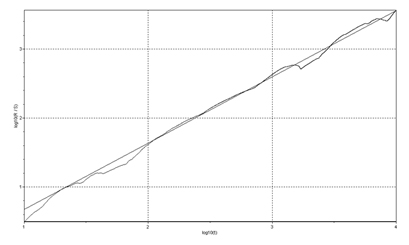
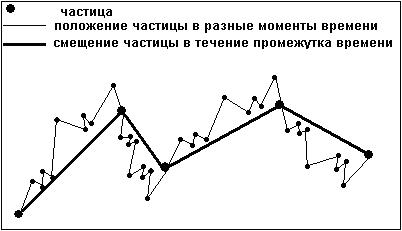
Волнистой линей изображен временной ряд (совокупность наблюдаемых параметров

изучаемой системы во времени) цен. Прямая линия представляет собой показатель Н (Херста) расположенную под углом со значением 0,5

Когда Н = 0,5 график будет соответствовать нормальному распределению и являться случайным. Если 0<Н< 0,5 , то процесс является антиперсистентным, — когда восходящая тенденция сменяется нисходящей или наоборот, т.е есть зависимость между движениями частиц (цен), но она является обратной. При 0,5<Н<1, процесс является персистентным, — если мы наблюдаем восходящую тенденцию то в будущем она продолжит свой рост.

Когда Н возрастает от 0,5 до 1, устойчивость становится все заметнее. С практической точки зрения это выражается в том, что возникающие разнородные «циклы» — не имеющие, не забываем, никакого периодического характера – различаются все яснее.

Неравенство Н>0,5 , исключает гипотезу о том что все величины являются независимыми и гауссовскими.

Обобщенное броуновское движение было введено Мандельбротом через обобщение случайной функции X(t) (случайные блуждания) путем замены показателя H = 0,5 на любое действительное число из интервала 0<Н<1.

Обобщенное броуновское движение – это класс гауссовских процессов позволяющих показателю Н принимать произвольные значения от 0 до 1.

О чем нам это может сказать? Все дело в том, что представление распределения цен в гауссовой модели (рис.5) отличается от цен представленных фрактальной моделью (рис.6): высоким пиком и толстыми хвостами. При этом функция с нормальным распределением (т.е гауссовская зависимость) имеет показатель Н = 0,5, тогда как функция соответствующая распределению цен, имеет показатель 0,5<Н <1. Получается, что, введя понятие обобщенного броуновского движения, Мандельброт показал, что при разнице свойств моделей, движение цены валютных пар представляет собой броуновское движение – обыкновенное или дробное. В зависимости от значения Н цена может обладать персистентными или антеперсистентыми свойствами.

Показатель Н – характеризует размерность (зазубренность временного ряда).

Н=0.2 – высокая размерность (антиперсистентность)

Н=0.9 – низкая размерность (персистентность)

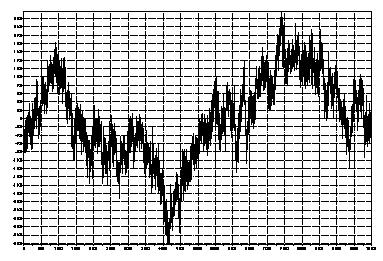
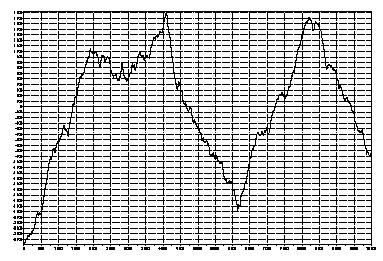
На рисунках, вы можете наблюдать дробное броуновское движение с различным значением Н. Показатель Херста описывает одно из свойств временного ряда и является достаточно интересным инструментом, для анализа валютной пары. В данной статье я не буду поднимать эту тему более подробно.

Помимо функции дробного броуновского движения, существует еще одна, называется она функция Вейерштрасса – Мандельброта. Данная функция была использована для изучения поведения конкретных моделей на Форекс и с помощью которой, было выявлено ряд свойств для анализа валютного рынка Форекс.

Рис.10

Рис.11

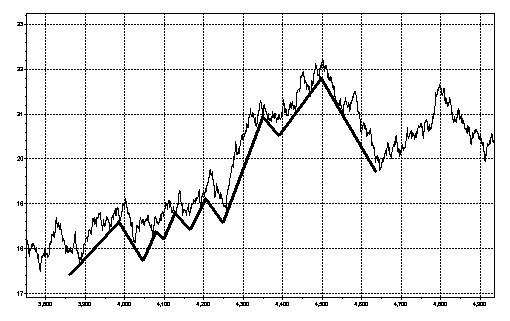
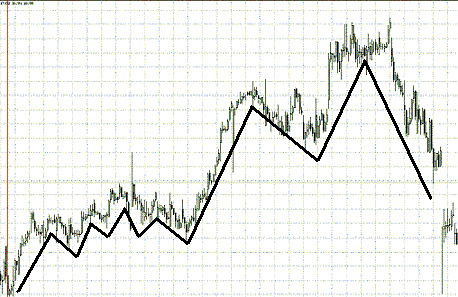
Как видно, с помощью данной функции можно получать очень реалистичные модели, которые в последствии можно применять для изучения поведения цены.

Мной разработана новая обучающая программа для трейдеров, торгующих на валютных, а также на других финансовых рынках. В цели данной программы входит ознакомление с моделью броуновского движения и, что самое важное, применение ее для прогнозирования финансовых рынков.

Благодаря развитию компьютерных технологий были созданы программы, с помощью которых стало возможным моделирование броуновского движения, одна из них Fractan. С недавнего времени, применяются индикаторы, которые моделируют структуру цены в on—line. Было выявлено, что после обучения, у трейдеров в значительной степени меняется восприятие биржевых цен, а также, что не мало важно, возрастает способность к их прогнозированию на различные временные периоды.

Скачать программу

© Алмазов Алексей Александрович.
© www.adamaz.ru — источник